
L'inquinamento luminoso è uno spreco di energia luminosa e quindi di energia elettrica, energia che deve essere prodotta o acquistata. Esso rappresenta quindi uno spreco di conbustibile e di denaro. È uno spreco di danaro per gli enti che gestiscono gli impianti di illuminazione, che spesso sono enti pubblici e quindi spendono denaro dei cittadini. Può essere uno spreco anche per l'ente che distribuisce l'energia elettrica, che deve produrre tale energia o acquistarla dall'estero.
Facciamo un esempio di come si può calcolare l'ordine di
grandezza dell'energia sprecata dagli impianti di illuminazione
esterna notturna. Facciamo l'ipotesi che in media una frazione
![]() dell'energia che esce da un punto luce sia disperso
in cielo. Possiamo quantificare lo spreco di energia in modo
approssimato moltiplicando il consumo annuo totale Q di energia
elettrica
dell'energia che esce da un punto luce sia disperso
in cielo. Possiamo quantificare lo spreco di energia in modo
approssimato moltiplicando il consumo annuo totale Q di energia
elettrica![]() in una nazione per la frazione che è stata utilizzata
per l'illuminazione esterna notturna fext . La quantità di
energia sprecata perché va a illuminare il cielo è quindi in
media per una nazione:
in una nazione per la frazione che è stata utilizzata
per l'illuminazione esterna notturna fext . La quantità di
energia sprecata perché va a illuminare il cielo è quindi in
media per una nazione:

(104)
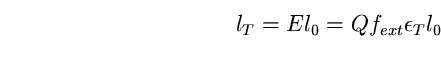
(105)

(106)

(107)

(108)
Consideriamo ora lo spreco costituito dall'uso di lampade a bassa
efficienza al posto di lampade ad alta efficienza. Sia qhg o
qj l'efficienza media in lumen/watt di una lampada ai vapori
di mercurio o agli Ioduri metallici, notoriamente lampade a bassa
efficienza. Sia qLPS l'efficienza media in lumen/watt di una
lampada al sodio a bassa pressione
(LPS) notoriamente una lampada
ad alta efficienza. Il rapporto X tra il numero di watt consumati
dalla lampada ai vapori di mercurio ( o agli ioduri metallici) per
produrre lo stesso flusso luminoso di una lampada al sodio a bassa
pressione e il consumo di quest'ultima, è:

(109)

(110)

(111)
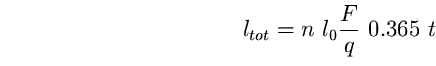
(112)
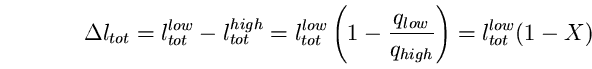
(113)
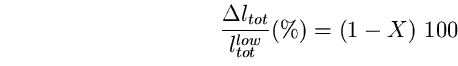
(114)
Per gli Stati Uniti, Hunter e Crawford (1991), sulla base di misure e modelli, hanno assunto che il 15% della luce emessa finisca direttamente in cielo e che un altro 15% ne venga inviato a causa della riflessione dalla superficie illuminata. Stimando nel 2.5% la percentuale della produzione di energia elettrica USA utilizzata nell'illuminazione esterna notturna, essi calcolano per l'illuminazione esterna notturna un consumo annuale di 58 miliardi di kilowatt/ora. Il 15% di tale quantità viene disperso direttamente in cielo. Si tratta di 8.7 miliardi di kilowatt/ora, equivalenti a 4.1 milioni di tonellate di carbone o a 15 milioni di barili di petrolio. Altri circa 8.7 miliardi di kilowatt/ora corrispondono a luce riflessa in cielo dalle superfici illuminate. Stimando un costo medio di 7.40 cents per kilowatt/ora, che però sale anche a 10.21 cents per kilowatt/ora nelle strade non residenziali e nelle autostrade, essi calcolano che la collettività spenda 644 milioni di dollari all'anno solo per illuminare il cielo notturno. Altrettanti 644 milioni di dollari vengono spesi per la luce riflessa dal terreno. Questa seconda spesa è in parte necessaria perché connessa con le necessità dell'illuminazione ma, in parte potrebbe essere diminuita con uno studio più attento della disposizione dei corpi illuminanti. Ad esempio evitando di illuminare gli edifici dal basso verso l'alto. I primi 644 milioni di dollari sono totalmente dilapidati.
Per quanto riguarda l'efficienza delle lampade, Crawford ha stimato che ci siano negli USA circa 10 000 000 lampade ai vapori di mercurio da 175 w, le quali funzionano mediamente 11.23 ore al giorno e consumano circa 210 w cosicché il loro consumo annuo è di circa 860 kwh. La loro efficienza è inferiore a 40 lm/w. Se esse fossero sostituite con lampade al sodio che arrivano ad efficienze anche di 140 lm/w, considerando che il costo dell'energia elettrica negli USA è, come abbiamo visto, in media sugli otto cent per kilowatt/ora, gli americani risparmierebbero oltre 500 milioni di dollari all'anno. E questo senza tener conto della maggior durata e quindi dei minori costi di manutenzione.
Per quanto riguarda la situazione dell'Italia possiamo stimare che per l'illuminazione esterna notturna siano stati impiegati nel 1994 dai 3 ai 6 miliardi di kwh. L'incertezza è dovuta alla difficoltà di calcolare con precisione la quantità di energia impiegata dagli impianti privati e la quantità di energia utilizzata per illuminazione pubblica non esterna. In base ai dati precedenti si può calcolare che il consumo di energia pro capite per l'illuminazione esterna notturna sia stato dell'ordine di 50-100 kwh annui. Assumendo approssimativamente, come Crawford, un accensione media di 11.2 ore al giorno, questo consumo corrisponde ad una potenza media di 12 - 24 w pro capite in accordo con i valori illustrati nella sezione 2.2. Come abbiamo visto in tale sezione, si stima che circa il 15% di questa energia sia consumata per produrre luce che finisce direttamente in cielo e costituisce uno spreco. Abbiamo visto nella sezione 2.2.3 che si stima altrettanta ne sia consumata per produrre luce che finisce in cielo a causa della riflessione delle superfici illuminate. Si può supporre che si potrebbe evitare che almeno una quantità di luce pari ad un terzo di quest'ultima finisca in cielo, senza creare danno al processo di illuminazione, se vi fosse maggior cura nel progetto degli impianti. In conclusione, la quantità di energia che si potrebbe risparmiare eliminando la dispersione di luce è dell'ordine del 20% del totale: si tratta di una quantità dell'ordine di un miliardo di kilowatt/ora ogni anno.
Calcoliamo ora, con il metodo illustrato, quale sarebbe il risparmio se l'efficienza media aumentasse, ad esempio, di un fattore 1.75, ossia se lampade con un efficienza di q=80 lm/w venissero sostituite da lampade con un efficienza q=140 lm/w o lampade con un efficienza q=40 lm/w da lampade con un efficienza q=70 lm/w. In questo caso il risparmio sarebbe pari al 43%. In conclusione, se risparmiassimo quella frazione di energia che corrisponde alla luce che viene dispersa in cielo (il 20%) e quella frazione di energia che viene consumata a causa della bassa efficienza della lampade (nel nostro esempio pari al 43%), il risparmio totale potrebbe essere superiore al 50%, ossia dell'ordine di alcuni miliardi di kilowatt/ora ogni anno, mantenendo gli stessi livelli di illuminazione al suolo.
Le nostre stime sono probabilmente per difetto. Ad esse va aggiunto il risparmio che si otterrebbe estendendo la parzializzazione, ossia lo spegnimento di certi impianti o la diminuzione della loro potenza negli orari in cui la potenza piena non è necessaria.
In termini economici, tenuto conto che il costo dell'energia elettrica per gli enti che gestiscono gli impianti è dell'ordine del centinaio di lire per kilowatt/ora o più, lo spreco di alcuni miliardi di kilowatt/ora ogni anno corrisponde ad una spesa inutile per enti pubblici e privati di alcune centinaia di miliardi di lire. Si parla di quattrocento miliardi sprecati nel 1994, in gran parte pagati dai contribuenti.