Vediamo come la luce viene diffusa![]() dalle particelle atmosferiche a
causa dei fenomeni illustrati nelle due precedenti sezioni.
dalle particelle atmosferiche a
causa dei fenomeni illustrati nelle due precedenti sezioni.
Chiamiamo ![]() l'angolo tra la direzione di propagazione della
luce e la direzione della diffusione. Possiamo definire un
coefficiente di diffusione
l'angolo tra la direzione di propagazione della
luce e la direzione della diffusione. Possiamo definire un
coefficiente di diffusione ![]() , chiamato anche funzione di diffusione , nel modo seguente:
, chiamato anche funzione di diffusione , nel modo seguente:
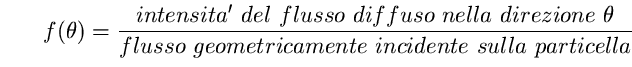
(20)
Vediamo qual é la forma![]() della funzione di diffusione
della funzione di diffusione ![]() di una particella.
di una particella.
La luce diffusa in direzioni vicine a quella della luce incidente
( frontscatter) è dovuta in gran parte alla diffrazione.
Poiché i fotoni diffratti non sono passati all'interno della
particella, essa è poco influenzata dall'indice di rifrazione
della particella ma dipende invece dalla sua forma e dalle dimensioni.
Teniamo fissa la lunghezza d'onda della luce incidente e
consideriamo la diffusione prodotta su particelle via via più
grandi. Per particelle molto piccole (![]() ) la funzione di diffusione è quella della diffusione Rayleigh
) la funzione di diffusione è quella della diffusione Rayleigh ![]() . Mano a mano che si considerano particelle di dimensioni
maggiori, la funzione di diffusione per effetto della
diffrazione diventa sempre più concentrata in un lobo molto stretto
attorno alla direzione che originalmente aveva la luce incidente.
Come le dimensioni crescono ed il parametro dimensionale
. Mano a mano che si considerano particelle di dimensioni
maggiori, la funzione di diffusione per effetto della
diffrazione diventa sempre più concentrata in un lobo molto stretto
attorno alla direzione che originalmente aveva la luce incidente.
Come le dimensioni crescono ed il parametro dimensionale ![]() supera l'unità, la funzione di diffusione inizia a sviluppare
picchi con una approssimativa corrispondenza tra il numero di
picchi tra 0truept
supera l'unità, la funzione di diffusione inizia a sviluppare
picchi con una approssimativa corrispondenza tra il numero di
picchi tra 0truept ![]() e 180truept
e 180truept ![]() ed
ed ![]() , sempre restando il
massimo ad
, sempre restando il
massimo ad ![]() . Quando
. Quando ![]() tende a 10 si sviluppa una
struttura ancor più fine e complessa. La figura 2.37
illustra quanto descritto.
tende a 10 si sviluppa una
struttura ancor più fine e complessa. La figura 2.37
illustra quanto descritto.
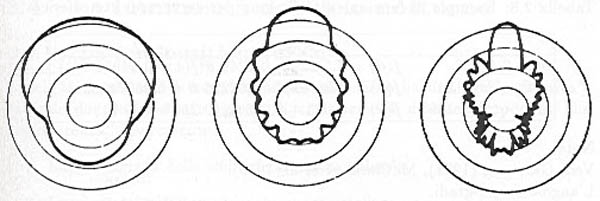
Figure 2.37:
Forma della funzione angolare di diffusione per tre particelle di
aerosol di dimensioni crescenti (0.1 ![]() , 0.6
, 0.6![]() , 1.2
, 1.2![]() ). Nella figura
la luce incidente proviene dal basso.
). Nella figura
la luce incidente proviene dal basso.
La radiazione diffusa nell'emisfero posteriore (backscatter) viene influenzata soprattutto dal coefficiente di assorbimento che costituisce la parte immaginaria dell'indice di rifrazione. Al crescere del coefficiente di assorbimento, essa decresce fino ad un minimo, oltre il quale aumenta di nuovo perché la particella diventa riflettente. Al crescere del coefficiente di assorbimento la asimmetria della diffusione diminuisce. Infatti, come abbiamo visto, l'emissione dovuta alla riflessione tende per particelle sferiche ad essere isotropa.
La forma della funzione di diffusione di una particella consiste quindi in un lobo più o meno stretto, molto intenso centrato nella direzione di propagazione della luce incidente che si sovrappone ad una emissione meno intensa di intensità variabile a seconda della direzione in base alle proprietà ottiche delle particella stessa.
L'effetto integrato di un volume di particelle, assumendo
che in esso avvenga una sola interazione tra luce e particella,
consiste nella
somma dei contributi delle varie particelle.
Le funzioni di Mie per questo elemento di volume si ottengono
dalla somma delle funzioni di Mie delle singole particelle, ammesso che
il numero di particelle sia elevato e la loro distribuzione sia
completamente casuale. Per luce non polarizzata quindi è
semplicemente:

(21)
Nel caso di un aerosol molto denso, come la nebbia, o in generale
quando la profondità ottica è molto maggiore di 1, la luce
diffusa da uno strato spesso subisce più di un interazione con
le particelle (scattering multiplo). In questo caso la funzione di diffusione che ne risulta è
piuttosto indipendente da quella originaria.
Le numerose interazioni successive cancellano i dettagli
strutturali lasciando un andamento molto
smorzato. Nebbia, nubi e aerosol non secchi hanno un maggior
frontscattering ripetto a quelli secchi, ma trasmettono meno la
luce. Per umidità maggiori del 70% si può assumere che la funzione di diffusione sia quella di una popolazione di
particelle sferiche![]() .
.
| 2|c| |
|
Spesso si usa definire un coefficiente detto sezione d'urto
angolare di diffusione, ![]() , espresso in unità di
superficie per particella per unità di angolo solido (es.
, espresso in unità di
superficie per particella per unità di angolo solido (es.
![]() per particella), che esprime la sezione (area)
del fascio incidente
che la particella diffonde in un'unità di angolo solido nella
direzione
per particella), che esprime la sezione (area)
del fascio incidente
che la particella diffonde in un'unità di angolo solido nella
direzione ![]() . Si definisce sezione d'urto integrata,
. Si definisce sezione d'urto integrata,
![]() , espressa in unità di superficie per particella, la
sezione del fascio incidente che viene diffusa in qualunque
direzione da una particella. Se la funzione di diffusione
, espressa in unità di superficie per particella, la
sezione del fascio incidente che viene diffusa in qualunque
direzione da una particella. Se la funzione di diffusione
![]() è normalizzata ad 1 per integrazione sulla sfera,
allora
è normalizzata ad 1 per integrazione sulla sfera,
allora ![]() .
.
Una tipica forma della funzione di diffusione per un volume di aerosol atmosferico si trova in tabella 2.8.