


Next: Magnitudini
Up: Le unità di misura
Previous: Unità energetiche
Abbiamo visto che il risultato della misura delle grandezze
precedenti è legata alla curva di sensibilità del sistema
che riceve la luce ed alla curva di emissione
della sorgente.
Sono state definite una serie di grandezze, chiamate
fotometriche, che si
riferiscono ad una distribuzione dell'emissione ben definita,
quella di un
corpo nero alla temperatura di solidificazione del platino (2045 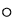 K).
K).
Le grandezze fotometriche si basano su una grandezza fondamentale
definita nel Sistema Internazionale SI, la candela. Essa è
definita come l'intensità luminosa (ossia il flusso per unità
di angolo solido) emessa da un corpo nero di Burgess alla
temperatura di solidificazione del platino (2045 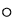 K) in
direzione perpendicolare al foro di uscita, quando la sezione di
un tale foro ha un area di 1/600000 m2 sotto la pressione di
101325 Pa (pascal).
K) in
direzione perpendicolare al foro di uscita, quando la sezione di
un tale foro ha un area di 1/600000 m2 sotto la pressione di
101325 Pa (pascal).
Il flusso luminoso 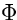 emesso in uno steradiante da una
sorgente puntiforme isotropa che abbia in quella direzione una
intensità pari ad una candela è detto lumen (lm).
Perciò,
l'intensità luminosa, cioè il flusso emesso nell'unità di
angolo solido,
emesso in uno steradiante da una
sorgente puntiforme isotropa che abbia in quella direzione una
intensità pari ad una candela è detto lumen (lm).
Perciò,
l'intensità luminosa, cioè il flusso emesso nell'unità di
angolo solido, 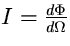 si può misurare in candele (cd) o in lumen per steradiante (
si può misurare in candele (cd) o in lumen per steradiante (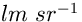 ).
).
La luminosità è definita come il flusso luminoso emesso nel
semispazio![[*]](foot_motif.gif) da un'area
unitaria di superficie irraggiante. Nel caso del cielo essa viene intesa
come il flusso proveniente da un emisfero e che finisce entro
un'area unitaria. L'unità della luminosità è il lambert (L) che
equivale ad un lumen per centimetro quadrato (lm/cm2 ):
da un'area
unitaria di superficie irraggiante. Nel caso del cielo essa viene intesa
come il flusso proveniente da un emisfero e che finisce entro
un'area unitaria. L'unità della luminosità è il lambert (L) che
equivale ad un lumen per centimetro quadrato (lm/cm2 ):

(48)
La brillanza o luminanza esprime il flusso luminoso emesso non in
tutto il semispazio ma nell'unità di angolo solido e nella
direzione da esso individuata, e non più da un'area unitaria ma
dalla proiezione di essa su un piano normale alla direzione della
luce. Nel nostro caso esprime anche il flusso emesso da una unità
di angolo solido di cielo entro un'area unitaria perpendicolare
alla direzione del flusso. Se la direzione del flusso e la normale
alla superficie fanno tra loro un angolo 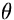 , la brillanza
è:
, la brillanza
è:

(49)
La brillanza si misura in lumen al metro quadro per
steradiante (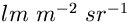 ) cioè in candele per metro
quadro (
) cioè in candele per metro
quadro (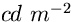 ).
Se una superficie irraggia in modo isotropo nel semispazio oppure
riceve luce in modo isotropo dal semispazio, allora ad una
brillanza di x
).
Se una superficie irraggia in modo isotropo nel semispazio oppure
riceve luce in modo isotropo dal semispazio, allora ad una
brillanza di x 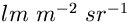 corrisponde, per la legge di Lambert, una
luminosità di
corrisponde, per la legge di Lambert, una
luminosità di 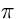 x
x 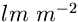 . In questo caso per ottenere la luminosità in nL
è sufficiente moltiplicare la brillanza, espressa in
cd/m2 , per il numero
. In questo caso per ottenere la luminosità in nL
è sufficiente moltiplicare la brillanza, espressa in
cd/m2 , per il numero 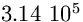 e per ottenere la
brillanza in cd/m2 è sufficiente moltiplicare la
luminosità in nL per
e per ottenere la
brillanza in cd/m2 è sufficiente moltiplicare la
luminosità in nL per 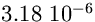 . Ad esempio una brillanza
media del cielo di
. Ad esempio una brillanza
media del cielo di 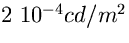 (Anon 1984) corrisponde ad
una luminosità di 62.8 nL. Attenzione che questa corrispondenza
tende a far confondere i concetti di luminosità e di brillanza.
Perciò quando qualcuno scrive "luminosità di x lambert allo
zenith" in realtà intende implicitamente riferirsi alla
luminosità che avrebbe il cielo se la sua brillanza fosse la
stessa in tutto l'emisfero ed uguale a quella allo zenith.
Allo stesso modo, quando qualcuno esprime la brillanza in lambert,
intende implicitamente esprimerla lumen per centimetro quadro per
(Anon 1984) corrisponde ad
una luminosità di 62.8 nL. Attenzione che questa corrispondenza
tende a far confondere i concetti di luminosità e di brillanza.
Perciò quando qualcuno scrive "luminosità di x lambert allo
zenith" in realtà intende implicitamente riferirsi alla
luminosità che avrebbe il cielo se la sua brillanza fosse la
stessa in tutto l'emisfero ed uguale a quella allo zenith.
Allo stesso modo, quando qualcuno esprime la brillanza in lambert,
intende implicitamente esprimerla lumen per centimetro quadro per 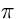 steradianti (
steradianti (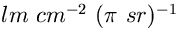 ) (v. ad es. Garstang 1986).
L'uso di esprimere la brillanza misurata allo zenith in questo
modo è giustificato dal fatto che si dà subito un idea della
luminosità totale del cielo.
L'autore consiglia di usare sempre, correttamente, la
brillanza (o luminanza) e di esprimerla in
) (v. ad es. Garstang 1986).
L'uso di esprimere la brillanza misurata allo zenith in questo
modo è giustificato dal fatto che si dà subito un idea della
luminosità totale del cielo.
L'autore consiglia di usare sempre, correttamente, la
brillanza (o luminanza) e di esprimerla in 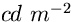 cioè in
cioè in
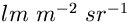 .
.
Un'altra quantità interessante è l'illuminamento, che si
riferisce non ad un flusso emesso come la luminosità ma ad un
flusso ricevuto, perpendicolarmente, per unità di area :

(50)
L'illuminamento si misura in lux (lx).
Un lux corrisponde all'illuminamento prodotto su una superficie
di un metro quadrato dal flusso di 1 lumen incidente
perpendicolarmente. Quindi 1 lx = 1 lm/m2 .
Se la superficie illuminata diffonde tutta la luce incidente,
senza assorbimenti, allora con un illuminamento di un lux essa
acquista una luminosità di un lumen per metro quadro, cioè
10-4 L (lambert) (il fattore 10-4 è dovuto al
passaggio tra m2 e cm2 ).
Conoscendo la curva di emissione di un corpo nero è
possibile calcolare il flusso di energia
corrispondente ad un certo flusso luminoso. Si trova che 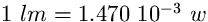 (v. ad es. Cook 1991).
Da questa relazione si ottiene la seguente formula di passaggio:
(v. ad es. Cook 1991).
Da questa relazione si ottiene la seguente formula di passaggio:
![\begin{equation}
b \left[ cd~m^{-2} \right] = 6.803~10^{2} ~~b \left[
w~m^{-2}~sr^{-1} \right] \end{equation}](images/img189.gif)
(51)
Dalla relazione precedente, con l'espressione 3.7, si può calcolare la relazione tra
lumen e fotoni al secondo per luce
monocromatica a 5550 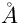 o per luce avente lunghezza d'onda
efficace di 5550
o per luce avente lunghezza d'onda
efficace di 5550 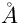 (come i fotoni della banda astronomica visuale) che è
(come i fotoni della banda astronomica visuale) che è 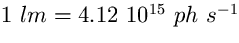 (v. Garstang 1986).
Con questa relazione si ottengono le seguenti formule di
passaggio per la brillanza:
(v. Garstang 1986).
Con questa relazione si ottengono le seguenti formule di
passaggio per la brillanza:
![\begin{equation}
b \left[ cd~m^{-2} \right] = 2.43~10^{-12}~n_{5550} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img191.gif)
(52)
![\begin{equation}
b \left[ cd~m^{-2} \right] = 1.935~10^{-7} ~~b \left[ Ry \right] \end{equation}](images/img192.gif)
(53)
Assumendo che la brillanza del cielo sia la stessa in ogni direzione, la luminosità è:
![\begin{equation}
l \left[ nL \right] = 7.634 ~10^{-7}~n_{5550} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img193.gif)
(54)
![\begin{equation}
l \left[ nL \right] = 6.075~10^{-2} b \left[ Ry \right] \end{equation}](images/img194.gif)
(55)
Poiché 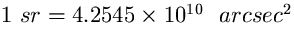 (v. ad es. Zombeck 2nd ed. 1990), è anche:
(v. ad es. Zombeck 2nd ed. 1990), è anche:
![\begin{equation}
l \left[ cd~m^{-2} \right] = 0.103~n_{5550} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img196.gif)
(56)
![\begin{equation}
l \left[ nL \right] = 3.248~10^{4}~n_{5550} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img197.gif)
(57)
La curva di sensibilità della banda astronomica V è
leggermente diversa dalla curva di sensibilità dell'occhio e dalla curva che definisce le grandezze fotometriche, per
cui, tenendo conto della sua minore larghezza, la relazione tra
lumen e fotoni al secondo in banda V è leggermente diversa dalla
precedente: 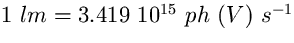 (Garstang
1989).
Da questa relazione si ottengono le seguenti formule di passaggio
per la brillanza:
(Garstang
1989).
Da questa relazione si ottengono le seguenti formule di passaggio
per la brillanza:
![\begin{equation}
b \left[ cd~m^{-2} \right] = 2.925~10^{-12}~n_{V} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img199.gif)
(58)
![\begin{equation}
l \left[ cd~m^{-2} \right] = 0.124~n_{V} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img200.gif)
(59)
Assumendo, come prima, che la brillanza del cielo sia la stessa in
ogni direzione, la luminosità è:
![\begin{equation}
l \left[ nL \right] = 9.184 ~10^{-7}~n_{V} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img201.gif)
(60)
![\begin{equation}
l \left[ nL \right] = 3.907 ~10^{4}~n_{V} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img202.gif)
(61)



Next: Magnitudini
Up: Le unità di misura
Previous: Unità energetiche
Pierantonio Cinzano
3/12/1998
![]() K).
K).
![]() K) in
direzione perpendicolare al foro di uscita, quando la sezione di
un tale foro ha un area di 1/600000 m2 sotto la pressione di
101325 Pa (pascal).
K) in
direzione perpendicolare al foro di uscita, quando la sezione di
un tale foro ha un area di 1/600000 m2 sotto la pressione di
101325 Pa (pascal).
![]() emesso in uno steradiante da una
sorgente puntiforme isotropa che abbia in quella direzione una
intensità pari ad una candela è detto lumen (lm).
Perciò,
l'intensità luminosa, cioè il flusso emesso nell'unità di
angolo solido,
emesso in uno steradiante da una
sorgente puntiforme isotropa che abbia in quella direzione una
intensità pari ad una candela è detto lumen (lm).
Perciò,
l'intensità luminosa, cioè il flusso emesso nell'unità di
angolo solido, ![]() si può misurare in candele (cd) o in lumen per steradiante (
si può misurare in candele (cd) o in lumen per steradiante (![]() ).
).
![]() da un'area
unitaria di superficie irraggiante. Nel caso del cielo essa viene intesa
come il flusso proveniente da un emisfero e che finisce entro
un'area unitaria. L'unità della luminosità è il lambert (L) che
equivale ad un lumen per centimetro quadrato (lm/cm2 ):
da un'area
unitaria di superficie irraggiante. Nel caso del cielo essa viene intesa
come il flusso proveniente da un emisfero e che finisce entro
un'area unitaria. L'unità della luminosità è il lambert (L) che
equivale ad un lumen per centimetro quadrato (lm/cm2 ):

![]() , la brillanza
è:
, la brillanza
è:


![]() (v. ad es. Cook 1991).
Da questa relazione si ottiene la seguente formula di passaggio:
(v. ad es. Cook 1991).
Da questa relazione si ottiene la seguente formula di passaggio:
![\begin{equation}
b \left[ cd~m^{-2} \right] = 6.803~10^{2} ~~b \left[
w~m^{-2}~sr^{-1} \right] \end{equation}](images/img189.gif)
![\begin{equation}
b \left[ cd~m^{-2} \right] = 2.43~10^{-12}~n_{5550} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img191.gif)
![\begin{equation}
b \left[ cd~m^{-2} \right] = 1.935~10^{-7} ~~b \left[ Ry \right] \end{equation}](images/img192.gif)
![\begin{equation}
l \left[ nL \right] = 7.634 ~10^{-7}~n_{5550} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img193.gif)
![\begin{equation}
l \left[ nL \right] = 6.075~10^{-2} b \left[ Ry \right] \end{equation}](images/img194.gif)
![\begin{equation}
l \left[ cd~m^{-2} \right] = 0.103~n_{5550} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img196.gif)
![\begin{equation}
l \left[ nL \right] = 3.248~10^{4}~n_{5550} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img197.gif)
![\begin{equation}
b \left[ cd~m^{-2} \right] = 2.925~10^{-12}~n_{V} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img199.gif)
![\begin{equation}
l \left[ cd~m^{-2} \right] = 0.124~n_{V} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img200.gif)
![\begin{equation}
l \left[ nL \right] = 9.184 ~10^{-7}~n_{V} \left[
ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img201.gif)
![\begin{equation}
l \left[ nL \right] = 3.907 ~10^{4}~n_{V} \left[
ph~cm^{-2}~s^{-1}~arcsec^{-2} \right] \end{equation}](images/img202.gif)